2D 要素は、全体 Y-Z 平面で入力する必要のある 3 節点 または 4 節点のアイソパラメトリック 3 角形または 4 辺形です。図 1 は、典型的な 2D 要素をいくつか示しています。図 2 が示すとおり、要素によって平面ソリッドまたは軸対称ソリッドを表現できます。どちらの場合でも、各要素節点には、2 並進自由度があります。軸対称ソリッドまたはシェルを表現するために要素を使用する場合、全体 Z 軸が回転軸になります。すべての要素は、+Y 半平面に存在している必要があります。この場合、Y は半径軸を表します。図 2 は、3 つの規則的内容を示しています。
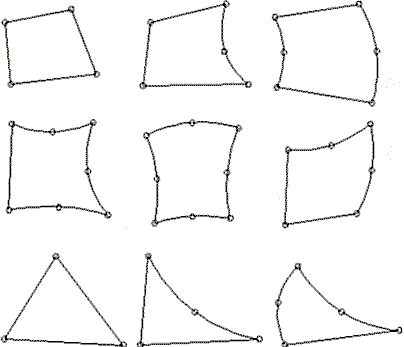
図 1: 2D 要素の節点設定
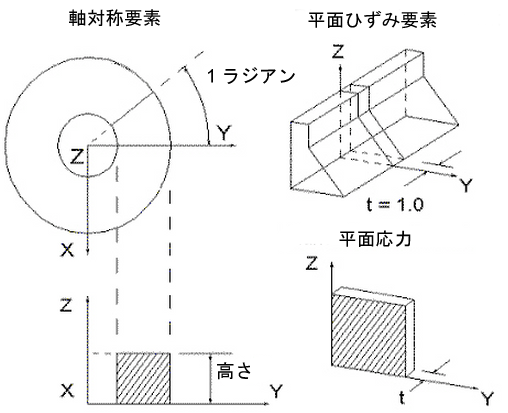
図 2: 2D 要素の適用
図 3: サンプル 2D 要素
2D 要素タイプの選択
非線形解析では、3 つのタイプの 2D 要素を使用できます。これらのタイプは、[要素定義]ダイアログの[一般]タブにある[幾何モデル タイプ]ドロップダウン ボックスで選択できます。
- [軸対称]: Z 軸を基軸とする対称的な幾何条件、荷重条件および境界条件を使用して固体をモデル化する要素に対して、この幾何モデル タイプを選択します。負の Y 座標は適格ではありません。節点が回転の軸(Z 軸)に沿ってある場合、Y 方向の移動を制約する必要があります。節点荷重は、円のラジアン数によって標準化されます(荷重をラジアンによって割る)。
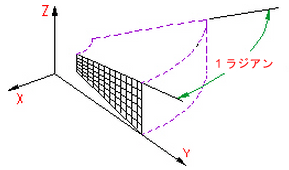
図 1: 2D 軸対称モデル
- [平面ひずみ]: この幾何モデル タイプは、YZ 軸に対して法線方向にあるたわみがないソリッドをモデル化する場合に選択します。X 方向にたわみが一切存在しないことが想定されるため、解析では 1 単位の厚さが想定されます。厚さは入力できますが、結果環境での 3D 可視化においてのみ使用されます。すべての入力荷重および結果は、1 単位の厚さに基づきます。

図 2: 2D 平面ひずみ
- 平面応力: YZ 平面に垂直な応力がなく、YZ 平面に垂直な厚さが指定されている固体のモデルを作成する際は、この幾何モデル タイプを選択します。構造的関係は、YZ 平面に垂直な応力が 0 になるように修正されます。厚さ全体にわたって、荷重はすべて均一に分布されます。
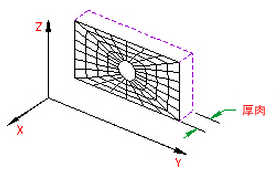
図 3: 2D 平面応力モデル
2D 要素パラメータ
まず最初に、[要素定義]ダイアログの[一般]タブにある[材料モデル]ドロップダウン ボックスを指定します。追加の入力パラメータの多くは、選択した材料モデルに依存します。利用可能な材料モデルは次のように分類されます。(各材料モデルの詳細については、「材料特性」ページの対応する箇所を参照してください。)
-
弾性
- [等方性]: この材料モデル オプションは、応力/ひずみ曲線の弾性領域のみでたわみが生じるパーツに対して使用します。この材料モデルを使用する場合、パーツでは、すべての方向で同一の材料特性が設定されている必要があります。単一のヤング率およびポアソン比が必須の材料特性となります。
- [直交異方性]: この材料モデル オプションは、応力/ひずみ曲線の弾性領域のみでたわみが生じるパーツに対して使用します。パーツでは、一定の方向に異なる材料特性を設定することができます。具体的には、長方形座標系の直交方向の 1 つまたは複数の方向で異なる材料特性を設定できます。
- [可変タンジェント]: この材料モデル オプションは、地質的材料の解析で使用します。このモデルは、体積弾性率やせん断弾性率が応力/ひずみ不変量の関数である、等方性の材料を記述します。
- [曲線]: この材料モデルは、地質的材料の解析で使用します。このモデルでは、瞬時的な体積弾性率やせん断弾性率は、現在の体積ひずみのパーツ単位の線形関数によって定義されます。
- [せん断曲線]: この材料モデル オプションは、上記の曲線材料モデルに似ています。ただし、いくつかの問題の解析では、適用荷重からの引張応力が重力の圧力を超えることができない点が異なります。その場合は、この材料モデルを使用して、重力の圧力を超える引張応力の方向において削減された剛性を想定する材料モデルなど、引張せん断をシミュレートすることができます。
- [温度依存等方性]: この材料モデルは、応力/ひずみ曲線の弾性領域のみでたわみが発生し、温度差によって応力が発生する可能性がある材料をモデル化する場合に使用します。
- [Duncan-Chang 粘土]: 粘土のシミュレートに Duncan-Chang (1970) モデルを使用します。このオプションは、3 軸の粘土テストに基づいており、双曲応力/ひずみ関係を想定します。この材料モデルを使用する場合、[幾何モデル タイプ]で[平面応力]を選択できません。さらに、[高度]タブの[解析定式化]を[非線形材料に限る]に設定します。
-
超弾性
- [Mooney-Rivlin]: この材料モデルは、ゴムなどの超弾性材料のモデル化で使用します。
- [Arruda-Boyce]: この材料モデルは、ゴム材料のモデル化に使用する超弾性材料モデルです。この実装は、体積保存変形モードに対する Ogden 材料の作用に従います。
- [Ogden]: この材料モデルは、ゴムなどの超弾性材料をモデル化する際に使用します。
- [Yeoh]: この材料モデルは、ゴムのようなほぼ非圧縮性(体積保存)の超弾性材料をモデル化する際に使用します。解析の定式化として使用できるのは、Total Lagrange 法のみです。
- [Neo-Hookean]: この材料モデルは、ゴムのようなほぼ非圧縮性(体積保存)の超弾性材料をモデル化する際に使用します。解析の定式化として使用できるのは、Total Lagrange 法のみです。
- [Van der Waals]: この材料モデルは、ゴムのようなほぼ非圧縮性(体積保存)の超弾性材料をモデル化する際に使用します。解析の定式化として使用できるのは、Total Lagrange 法のみです。
-
[フォーム材]
- [Blatz-Ko]: この材料モデルでは、体積弾性率のように、体積パーツと非体積パーツとの強力な結合が発生します。その他の超弾性材料モデルと同様、個別に決定できません。
- [Hyperfoam]: この材料モデルは、Ogden 材料モデルに類似した超弾性材料に使用します。この材料モデルは、材料の圧縮率を考慮します。平面ひずみ要素には適用できません。
-
粘弾性
- [粘弾性 Mooney-Rivlin]: Mooney-Rivlin (超弾性)材料モデルの粘弾性バリエーションです。
- [熱クリープ粘弾性]: この材料モデルは、応力/ひずみ曲線の弾性領域のみでたわみが発生し、クリープが発生する可能性がある材料をモデル化する場合に使用します。クリープは、時間の経過と共に一定荷重によってモデルがたわんだ状態になると発生します。「2D 要素の熱特性を定義する」を参照して、この材料モデルで使用するクリープ則を設定します。
- [粘弾性 Arruda-Boyce]: Arruda-Boyce (超弾性)材料モデルの粘弾性バリエーションです。
- [粘弾性 Blatz-Ko]: Blatz-Ko (超弾性)材料モデルの粘弾性バリエーションです。
- [粘弾性 Ogden]: Ogden (超弾性)材料モデルの粘弾性バリエーションです。
- [粘弾性 Hyperfoam]: ハイパーフォーム材料モデルを粘弾性に応用したものです。
- [線形粘弾性等方体]: 材料が弾性ソリッドおよび粘性流体の特性を示す粘弾性材料モデルです。粘弾性特性は Prony 級数に基づきます。この特性はすべての方向で等しく(等方性)、温度に依存しません。
- [線形粘弾性直交異方性]: 材料が弾性ソリッドおよび粘性流体の特性を示す粘弾性材料モデルです。粘弾性特性は Prony 級数に基づきます。この特性は 3 つの垂直方向で異なり(直交異方性)、温度に依存しません。
- [線形熱粘弾性等方体]: 材料が弾性ソリッドおよび粘性流体の特性を示す粘弾性材料モデルです。粘弾性特性は Prony 級数に基づきます。特性は、すべての方向で等しく(等方性)、温度に依存します。
- [粘弾性 Neo-Hookean]: Neo-Hookean (超弾性)材料モデルの粘弾性バリエーションです。
- [粘弾性 Yeoh]: Yeoh (超弾性)材料モデルの粘弾性バリエーションです。
- [粘弾性 Yeoh]: Van der Waals (超弾性)材料モデルの粘弾性バリエーションです。
-
塑性
- [Hardening 等方硬化をともなうフォンミーゼス]: この材料モデル オプションは、解析中に塑性変形が発生する可能性があるパーツで使用します。双線形曲線を使用して応力-ひずみ関係を表します。
- [移動硬化によるフォン ミーゼス]: この材料モデル オプションは、解析中に塑性変形を示すパーツに使用します。双線形曲線を使用して応力-ひずみ関係を表します。モデルで循環荷重が発生する場合は、[Hardening 等方硬化をともなうフォンミーゼス]材料モデル オプションに対してこの材料モデル オプションの使用を優先します。
- [Hardening 等方硬化をともなうフォンミーゼス曲線]: この材料モデル オプションは、解析中に塑性変形が発生する可能性があるパーツで使用します。応力-ひずみ関係を表すために、複数のデータ ポイントを持つ応力-ひずみ曲線を指定できます。
- [移動硬化によるフォン ミーゼス曲線]: この材料モデル オプションは、解析中に塑性変形を示すパーツに使用します。応力-ひずみ関係を表すために、複数のデータ ポイントを持つ応力-ひずみ曲線を指定できます。モデルで循環荷重(Bauschinger 効果)が発生する場合は、[Hardening 等方硬化をともなうフォンミーゼス]材料モデル オプションに対してこの材料モデル オプションの使用を優先します。
- [温度依存の塑性]: この材料モデルは、解析中の塑性変形、温度差による応力が発生する可能性がある材料をモデル化する場合に使用します。
-
[粘塑性]
- [熱クリープ粘塑性]: この材料モデルは、塑性変形を示し、かつクリープも示す可能性がある材料をモデル化する際に使用します。クリープは、時間の経過と共に一定荷重によってモデルがたわんだ状態になると発生します。「2D 要素の熱特性を定義する」を参照して、この材料モデルで使用するクリープ則を設定します。
- [Drucker-Prager]: この材料モデルは、フォンミーゼス材料モデルに似ていますが、降伏関数が追加されてています。このモデルでは、体積ひずみにより降伏関数が変化するものとみなします。これは、コンクリートや石などの材料で発生します。
[幾何モデル タイプ]: [幾何モデル タイプ]ドロップダウン ボックスを使用して幾何タイプを選択します。平面応力または平面ひづみの幾何タイプを使用する場合、[要素定義]ダイアログの[厚さ]フィールドでパーツの厚さを定義する必要があります。
このパーツで、中間節点をアクティブにする必要のある 2D 要素には、[中間節点]ドロップダウン ボックスの[含む]オプションを選択します。このオプションを選択すると、2D 要素では、各エッジの中間点に追加の節点が定義されます。これにより、4 節点の 2D 要素が 8 節点の 2D 要素に変更されます。中間節点を含む要素では、より正確に計算された勾配が結果として生じます。要素に中間節点が含まれる場合、処理時間が長くなります。メッシュが十分に小さい場合は、中間節点を追加しても正確度がそれほど向上しないこともあります。
[解析タイプ]ドロップダウンを使用して、目的とする変位のタイプを設定します。[微小変形]は、運動がなく、小さなひずみしか受けないパーツに適しています。この場合、大きな変形の結果生じた非線形の幾何学的影響は無視されます (これにより、[高度]タブの[解析の定式化]が[非線形材料に限る]に設定されます) 。[大変形]は、運動や大きなひずみを受けるパーツに適しています ([高度]タブの[解析定式化]を、解析に必要な設定にすることも必要です。)
- 中間節点における変位は常に出力されます。中間節点における応力とひずみは、ユーザにより解析の実行前にこれらの結果を出力するオプションがアクティブにされている場合にのみ出力されます。このオプションは、[出力]タブの[設定]
 [モデル設定]
[モデル設定]  [パラメータ]
[パラメータ]  [高度]ダイアログにあります。(詳細については、「出力ファイルを制御する」ページを参照してください)
[高度]ダイアログにあります。(詳細については、「出力ファイルを制御する」ページを参照してください) 
 [オプション]
[オプション] [解析]タブを使用して、[非線形解析のための既定として大変形を使用]オプションを使用して、[解析タイプ]の既定を小変形または大変形に設定します。
[解析]タブを使用して、[非線形解析のための既定として大変形を使用]オプションを使用して、[解析タイプ]の既定を小変形または大変形に設定します。
2D 要素の方向を制御する
2D 要素には、要素軸と材料軸の2つの軸があります。次の説明では、要素軸を Elem1 および Elem2、材料軸を Mat1 および Mat2 として指定します。この文書のその他のセクションでは、軸 1 および 2 として設定されています。
一般的な FEA 解析では、要素の方向(Elem1 および Elem2)を無視できます。要素の方向設定機能は、直交性材料モデルの要素で使用すると便利です。これは、[要素定義]ダイアログの[方向]タブで設定します。[方法]ドロップダウン ボックスには、要素のどちら側面が ij 側になるのかを指定する場合に使用できる 3 つのオプションがあります。[既定]オプションを選択すると、最も高いサーフェス番号を持つ要素の側面が ij 側として選択されます。[I 節点方位]オプションを選択すると、[X 座標]、[Y 座標]および[Z 座標]フィールドで座標を定義する必要があります。この点に最も近い要素の節点が、i 節点として指定されます。j 節点は、反時計周りに移動する要素の次の節点になります(+X 軸に対する右手の法則)。[IJ 辺の方位]オプションを選択すると、[Y 座標]および[Z 座標]フィールドで座標を定義する必要があります。この点に最も近い要素の側面が、ij 側として指定されます。i および j 節点が割り当てられるため、要素に沿って反時計回りに移動することで、i 節点から j 節点に達することができます。
ij 側が決定すると、要素軸 Elem1 は ij 側に対して平行に設定されます。軸 Elem2 は、X 軸に対して +90 度です。図 1 を参照してください。
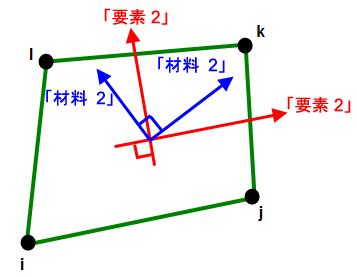
図 1: 要素軸と材料軸
要素軸 1 は、要素の ij エッジに対して平行です。
材料軸 Mat1 は、要素軸からオフセット設定できます。
[材料軸方向]: 2D 要素で直交性材料モデルを使用する場合、3 つの材料軸を定義します。材料軸 Mat1 および Mat2 は、要素の平面にあり、Mat3 は、X 軸に対して平行です。
[要素定義]ダイアログの[一般]タブでは、2 つの方法で材料軸を定義できます。最初の方法では、[X 方向]、[Y 方向]、[Z 方向]フィールドを使用して、ベクトルを定義します。材料軸 1 は、全体ベクトルに対して平行です。材料軸 2 は、X 軸と材料軸 1 のクロス積になります。図 2 および 3 は、この方法を示しています。[Y 方向]または[Z 方向]フィールドに値を指定しない場合、要素軸 Elem1 に対して相対的な材料軸の方向を設定するため[材料軸回転角]フィールドの値が使用されます。これは、パーツが元のシートから特定の形状に成型されている場合に便利です。回転角度βは、各要素の要素軸 1 に対して相対的な材料軸 1 の角度に対応します。図 4 を参照してください。
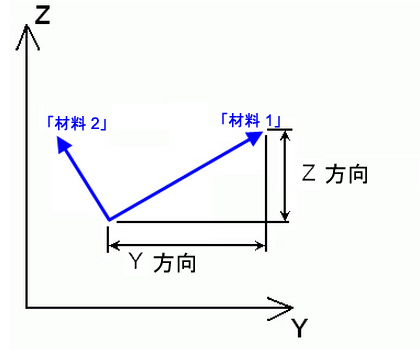
図 2: 材料軸の方向の Y および Z 方向の定義
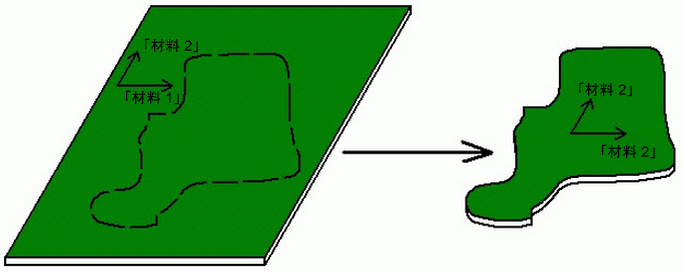
図 3: 直交性材料からカット アウトされたパーツ
メッシュがランダムになり、その結果、ランダムな要素軸が発生しますが、材料軸は一貫しています。
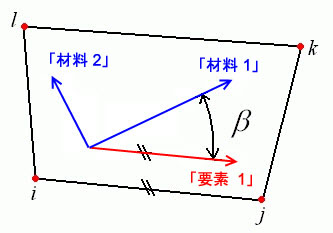
図 4: 材料軸の方向の回転角度の定義
2D 要素の熱特性の定義
熱セクション
2D 要素のパーツで温度効果を持つ材料モデルを使用している場合、[要素定義]ダイアログの[熱]タブにある[応力なしの参照温度]フィールドに値を指定する必要があります。この値は、節点温度の双線形補間を使用して熱増加の拘束に関連する要素ベースの荷重を算出するための参照温度として使用されます。
クリープ セクション
2D 要素のパーツでクリープを含む材料モデルを使用している場合、[クリープ則]ドロップダウン ボックスでオプションを選択します。この選択は、解析中にクリープ効果を計算するために使用されます。使用可能なクリープ則は次のとおりです。
- [クリープなし]: このオプションを選択すると、解析にクリープ効果は追加されません。
- [べき乗則]: このオプションは、単軸クリープ則とも呼ばれます。この式は、
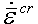 = C
1
x
= C
1
x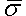 C2
x t
C3
で表されます。
C2
x t
C3
で表されます。 - [Garofalo]: このオプションは、双曲線正弦クリープ則とも呼ばれます。この式は、
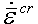 = A
0
x [sinh(A
1
x
= A
0
x [sinh(A
1
x 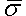 )]
A2
で表されます。
)]
A2
で表されます。 - [二重べき乗則]: このオプションはべき乗則と似ていますが、高応力レベルでの実験結果に近い結果を出すための項が追加されています。この式は、
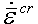 = C
1
x
= C
1
x 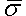 C
2
x t
C3
+ C
4
x
C
2
x t
C3
+ C
4
x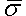 C5
x t
C6
で表されます。
C5
x t
C6
で表されます。
ただし、![]() は有効クリープひずみ速度、
は有効クリープひずみ速度、![]() は有効応力です。材料特性の入力に関する重要な情報については、「熱クリープ粘弾性材料特性」ページを参照してください。
は有効応力です。材料特性の入力に関する重要な情報については、「熱クリープ粘弾性材料特性」ページを参照してください。
均一の大きさに分割された時間ステップでクリープ計算が行われるようにする場合は、[時間積分法]ドロップダウン ボックスで[固定サブステップ]オプションを選択します。不定の大きさに分割された時間ステップでクリープ計算が行われるようにする場合は、[可変サブステップ]オプションを選択します。この 2 つの方法は時間硬化則に基づいており、陽的時間積分法が使用されます。これらの方法は、荷重状態によっては不安定になる場合があります。熱クリープ粘弾性材料モデルを使用する場合、[時間積分法]ドロップダウン ボックスで[α法]という追加のオプションを使用できます。. この方法は、暗黙的な時間積分スキーマを使用してクリープ動作を向上させます。この方法は無条件に安定します。
熱応力が存在しない温度を[応力なしの参照温度]フィールドで指定します。
[クリープひずみの定義]ドロップダウン ボックスの[有効]オプションは、非循環荷重の解析に適しています。
解析時、クリープ計算は、各時間ステップのサブステップにおける反復として実行されます。[サブステップの最大数]フィールドでは、単一の時間ステップで許可するサブステップの数を制御できます。単一のサブステップで実行可能な反復数を[サブステップにおける反復の最大数]フィールドで指定することもできます。各サブステップの反復の後、クリープ応力とひずみが前回の反復と比較されます。この値が、[クリープひずみ計算の許容誤差]と[クリープ応力計算の許容誤差]の各フィールドに指定した許容誤差の範囲にない場合は、もう一度反復を実行する必要があります。
α法の時間積分法では、[時間積分パラメータ]を指定する必要があります。完全に明示的な時間積分法(ただし、固定した/固定しないサブステップの明示的方法とは異なる)を使用する場合は、[時間積分パラメータ]フィールドに 0.0 を入力します。完全に暗黙的な時間積分法を使用する場合は、[時間積分パラメータ]フィールドに 1.0 を入力します。[時間積分パラメータ]が 0.5 よりも大きい場合、この方法は状態に左右されずに安定します。
高度な 2D 要素パラメータ
[高度]タブの[解析定式化]ドロップダウン ボックスを使用して、2D 要素に使用する定式化方法を選択します。
- [非線形材料に限る]オプションを選択すると、非線形材料モデルの効果は考慮されますが、すべての計算は変形していないジオメトリに基づき実行されます。したがって、この定式化は、小さなひずみを受け、運動がないパーツに適しています。これは、[一般]タブの[解析タイプ]が[微小変形]に設定されている場合、使用可能な唯一のオプションです。
- [Total Lagrange 法]オプションを選択すると、すべての静的変数および運動学変数について、初期状態で変形されていないモデルの構成が参照されます。この定式化は、運動と小さなひずみを受けるパーツに適しています。材料特性は、エンジニアリングにおける応力およびひずみである点に注意が必要です。
- [Updated Lagrangian 法]では、すべての静的変数および運動学的変数に対して、モデルの最後に計算された形状が参照されます。 この定式化は、運動と大きななひずみを受けるパーツに適しています。材料特性は、実際の応力とひずみについてであることに注意してください。
次に、このパーツの 2D 要素で使用する積分オーダを[積分オーダ]ドロップダウン ボックスで選択します。長方形の要素には、[第 2 オーダ]を選択します。中程度に変形した要素には、[第 3 オーダ]を選択します。過度に変形した要素には、[第 4 オーダ]を選択します。要素剛性の定式化にかかる計算時間は、積分オーダの 3 乗に比例して増大します。したがって、受け入れ可能な結果を生成する最も低い積分オーダを使用すると、処理時間を短縮できます。
[応力更新法]は、材料モデル([一般]タブ)を次のいずれかの塑性材料モデルに設定する場合に使用します。
- [等方硬化をともなうフォンミーゼス]
- 移動硬化によるフォン ミーゼス
- [等方硬化をともなうフォンミーゼス曲線]
- [等方硬化をともなうフォンミーゼス曲線]
この設定により、材料が塑性を示すときの構成方程式(応力/ひずみ則)を積分するための数値アルゴリズムを指定できます。[応力更新方法]で使用可能なオプションは次のとおりです。
- [陽解法]: (独自手法)。 このオプションでは、構成方程式の積分に陽的サブ増分前進オイラー法を使用します。[陽解法]オプションは、実行時間が短いので単純引張などの単純な問題に最適です。ただし、荷重および時間ステップのサイズの影響を受けやすい方法でもあります。
- [一般化された中点法]: このオプションでは、構成方程式の積分に陰解法を使用します。この方法では累積誤差が減少し、応力更新プロセスが無条件に安定します。そのため、接触問題や強塑性などの複雑な解析に適しています。
[一般化中間点のためのパラメータ]は、[応力更新法]を[一般化された中点法]に設定したときに入力します。0 以上 1 以下の範囲で入力することができます。パラメータを 0 (ゼロ)に設定した場合、完全陽解法のいずれかのアルゴリズムが得られます([応力更新方法]で[陽解法]オプションに設定した場合と同じ)。ただし、解法は無条件に安定ではありません。パラメータを 0.5 以上に設定した場合、解法は無条件に安定します。パラメータを 0.5 に設定した場合の解法は中間点アルゴリズムとして知られています。1 に設定した場合の解法は完全後退オイラー法または最接近点アルゴリズムとして知られており、完全陰解法です。1 の値はその他の値に比べより精度が高く、大きな時間ステップの場合は特にそうです。
[ひずみ測定]は、[材料モデル]([一般]タブ)を[等方性]に設定し、[解析定式化]を[Updated Lagrangian 法]に設定した場合に使用します。このオプションを使用すると、Updated Lagrangian 法の収束が向上します。 [ひずみ測定]では、次のオプションが使用可能です。
- [Almansiのひずみ]: (元来の方法)このオプションでは、構成関係に Cauchy 応力と Almansi のひずみを使用します。小ひずみの問題にのみ使用できます。
- [対数ひずみ]: このオプションでは、構成関係に Cauchy 応力と仮想対数ひずみ(増分ひずみ)を使用します。大ひずみを含め、すべての問題に使用できます。これは亜弾性モデルであり、圧縮性材料よりも非圧縮性材料(ポアソン比が 0.5)に適しているという難点があります。これは、せん断弾性係数が、現実では体積の変動によって変化するにも関わらず、一定であると想定されるからです。
[要素の重なりを許可]チェックボックスをアクティブにすると、線形を要素に変換する場合に重り合った要素の作成が許可されます。要素をモデル化する際に重なりが必要となることがあります。このことは、平面上での動きに限定される問題に特に該当します。
各要素の応力の結果が、解析時の各タイム ステップにおいてテキスト ログ ファイルに書き込まれるようにするには、次のことを行います。[詳細な応力出力]チェック ボックスをアクティブにします。その場合、出力の量が大きくなる場合があります。
フォンミーゼス材料モデルのいずれかを選択した場合、現在の材料の状態(弾性または塑性)、現在の降伏応力制限、現在の等価応力制限および角の節点の等価塑性ひずみ出力、および/または各時間ステップの統合ポイントを含むよう選択できます。これは、[追加の出力]ドロップダウン メニューで適切なオプションを選択して行います。
土条件の定義
Duncan-Chang 材料モデルを選択した場合は、[土]タブが有効になります。解析に応じて次のオプションを設定します。この入力は土壌の初期状態に関連しています。詳細については、「Duncan-Chang の理論的説明」ページを参照してください。
- [静水圧を付加]: このオプションをオンにすると、入力フィールドに設定した一定の静水圧に基づき初期応力が作成されます。(この場合の静水圧はすべての方向に等しく作用します。深さの増加に伴い増大する水圧と混同しないでください。)圧力の大きさは 0 (ゼロ)より大きくする必要があります。
- [自身の重量を付加]: このオプションをオンにすると、モデル化された土壌の重量に基づき初期応力が作成されます。
- [サーフェスの基準点]: X、Y、Z 座標を指定します。これにより、土壌の重量による圧力がゼロになる位置が決まります。モデルが地下深くの土の断面である場合、 基準点はモデル化したパーツの上に設定できます。
- [側面土圧の係数]: ほとんどの土壌では、真の(すべての方向に大きさが等しい)静水圧は発生しません。水平方向の応力は、通常、垂直方向の応力の一部しかありません。横応力と垂直応力との比率によって側面土圧の係数が決まります。入力値は 0 ~ 1 の範囲で指定する必要があります。
- [重力加速度]: 自身の重量による応力分布を作成するには、重力定数、および応力分布が発生するために作用する重力の方向を入力します。この方向は、通常、解析での重力の方向と同じです。ただし、初期応力が作成された時点やモデルの現在の方向とは別の方向に土壌が表されている場合は、別の方向を使用することもできます。土が移動されています。
損傷解析タイプの定義
[材料モデル]が[直交異方性]で、[幾何モデル タイプ]が[平面応力]である場合、[損傷]タブが有効になります。
損傷モデルは、弾性-脆性直交異方性材料の損傷の発生および進行的拡大をシミュレートします。モデルは、主に繊維強化の複合材料をシュミレートする目的で使用されます。その他の計算の詳細については、「損傷の理論的記述」ページを参照してください。
損傷モデルは、材料非線形のみおよび Total Lagrangian 法の解析定式化で機能しますが、Updated Lagrangian 法では機能しません。
選択可能な損傷開始条件は、次のとおりです。
- [なし]: 損傷計算を実行しません。
- [損傷の開始]: パーツ内での損傷発生の有無および場所を計算します。ただし、損傷の開始後の発生内容は計算されません。繊維の引張基準(fI)、繊維の圧縮基準(fII)、母材の引張基準(fIII)、および母材の圧縮基準(fIV)が計算されます。
- [損傷の開始と進展]: 損傷発生後の内容を計算します。損傷が発生すると、要素の剛性が減少します。先ほどの計算済み値に加え、繊維の引張損傷(dft)、繊維の圧縮損傷(d fc )、母材の引張損傷(dmt)、母材の圧縮損傷(dmc)、損傷エネルギー密度(ΔED)が計算されます。
- [損傷の開始と安定的進展]: 損傷後の効果が必要な場合は、直前の方法を使用します。ただし、突然の剛性損失によって損傷が発生した場合、解析が不安定になる場合があります。この方法を選択すると、解法を安定させるために粘性正則化(Duvaut-Lions)が追加されます。これはあくまでも人工的であるため、安定した解法に必要な最小限の粘性を使用します。解析後、損傷エネルギー密度の結果を粘性エネルギー密度の結果と比較します。粘性効果を無視するには、粘性エネルギー密度が損傷エネルギー密度に比べ非常に小さくなければなりません。先ほどの計算済みの値に加え、粘性エネルギー密度(ΔE
V
)が計算されます。このオプションを選択すると、次の入力項目が[損傷安定化の粘性パラメータ]セクションで有効になります。
- [局部 1 (引張)]: 繊維の引っ張り(ηft)のモードの粘性係数
- [局部 1 (圧縮)]: 繊維の圧縮(ηfc)のモードの粘性係数
- [局部 2 (引張)]: 母材の引っ張り(ηmt)のモードの粘性係数
- [局部 2 (圧縮)]: 母材の圧縮(ηmc)のモードの粘性係数
2D 要素の使用の基本手順
- 単位系が定義されていることを確認します。
- モデルで非線形解析タイプを使用していることを確認します。
- 2D 要素に設定するパーツの[要素タイプ]の見出しを右クリックします。 ヒント: 3D モデルを 2D モデルに変換する際は、 [作成]
 [パターン]
[パターン] [再配置と尺度]コマンド、 [作成]
[再配置と尺度]コマンド、 [作成] [パターン]
[パターン] [回転またはコピー]コマンド、[作成]
[回転またはコピー]コマンド、[作成]  [変更]
[変更] [平面に投影]コマンドが有効です。たとえば、誤って XY 平面にメッシュを作成したとします。[再配置と尺度]または[回転]コマンドのいずれかを使用してメッシュを YZ 平面に回転できます。計算の丸めにより、節点が小さな X 座標値を持ち、その要素タイプが 2D に設定されないことがあります。この場合は、[平面に投影]を使用して、節点を YZ 平面に正確にスナップさせます。
[平面に投影]コマンドが有効です。たとえば、誤って XY 平面にメッシュを作成したとします。[再配置と尺度]または[回転]コマンドのいずれかを使用してメッシュを YZ 平面に回転できます。計算の丸めにより、節点が小さな X 座標値を持ち、その要素タイプが 2D に設定されないことがあります。この場合は、[平面に投影]を使用して、節点を YZ 平面に正確にスナップさせます。 - [2D]コマンドを選択します。
- [要素定義]の見出しを右クリックします。
- [要素定義を編集]コマンドを選択します。
- [一般]タブで、[材料モデル]ドロップダウン ボックスから適切な材料モードを選択します。
- [幾何モデル タイプ]ドロップダウン ボックスで適切な幾何タイプを選択します。
- [幾何モデル タイプ]ドロップダウン ボックスで[平面応力]または[平面ひずみ]オプションを選択した場合は、2D 要素の厚さを入力します。
- 熱効果またはクリープ/粘弾性効果を含む材料モデルを選択した場合は、[熱]タブで必要情報を指定します。
- [OK]ボタンを押します。