El primer paso en el ajuste de una topografía horizontal es el cálculo de C, la matriz de coordenadas, con las coordenadas aproximadas para todos los P.K.
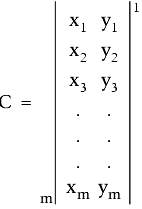
A continuación, se calcula la matriz L basada en las observaciones calculadas que se derivan de la matriz de coordenadas, C, y las observaciones medidas. La siguiente fórmula se utiliza para determinar cada valor de observación Li:
donde:
- Omeas = la observación según se ha medido
- Ocalc = la observación según se ha calculado
La matriz L aparece como se indica a continuación:
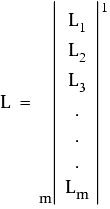
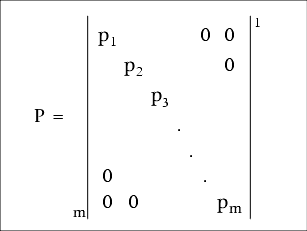
A continuación, la matriz de pesos diagonal, P, se calcula basada en desviaciones estándar de distancias y ángulos. Las siguientes fórmulas se utilizan para resolver 
, el valor de distancia ponderada, y 
, el valor angular ponderado:
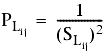
donde:
es la desviación estándar de la longitud ij
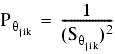
donde:
es la desviación estándar del ángulo jik
El último paso consiste en calcular la matriz A, que relaciona los cambios de las coordenadas con cada observación determinada mediante el uso de ecuaciones de observación de distancia y ecuaciones de observación de ángulo o acimut/orientación. En principio, estas ecuaciones son no lineales, de manera que la aproximación de series de Taylor se utiliza para renderizarlas como ecuaciones lineales.