Para ajustar aún más la precisión de este proceso, también se puede dibujar una elipse de error normalizada. Mediante una distribución F de las estadísticas aplicadas, se crea una elipse de error de probabilidad del 95% o 99%. Esta elipse presenta arcos tangentes a los lados del rectángulo de error, una orientación está determinada por un ángulo, t, y ejes auxiliares ortogonales u-v. De nuevo, los valores de la matriz de covarianza se utilizan para calcular el ángulo t y los semiejes mayor y menor asociados.
En primer lugar se resuelven tres variables para utilizarlas en ecuaciones que determinen los semiejes mayor y menor: K, Quu y Qvv.
Se utilizan las siguientes fórmulas:
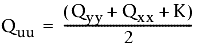
y
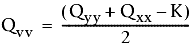
Donde
- Qxx, Qyy y Qxy son valores de la matriz de covarianza.
A continuación, estos valores se utilizan para resolver dos ecuaciones y poder determinar el valor de Su, la longitud del semieje mayor, y Sv, la longitud del semieje menor:
y
Donde
- So = desviación estándar de peso de unidad
Para finalizar, el ángulo t, que forma el eje u con el eje Y, se resuelve con la siguiente ecuación:
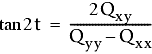
Lo más probable es que el punto ajustado se encuentre dentro de esta elipse con un grado de fiabilidad del 95% o 99%.