Per perfezionare il processo, è anche possibile disegnare un'ellisse d'errore standard. Se si utilizza una distribuzione F delle statistiche applicate, viene creata un'ellisse d'errore al 95% o al 99% di probabilità. Questa ellisse presenta archi tangenti ai lati del rettangolo d'errore e l'orientamento determinato dall'angolo t e dagli assi u-v ortogonali ausiliari. Anche questa volta i valori della matrice di covarianza vengono utilizzati per calcolare l'angolo t e i semiassi principale e secondario associati.
Innanzitutto, risolvere le tre variabili da utilizzare nelle equazioni che determinano i semiassi principale e secondario: K, Quu e Qvv.
Vengono utilizzate le seguenti formule:
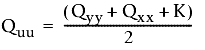
e
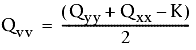
dove
- Qxx, Qyy e Qxy sono i valori derivati dalla matrice di covarianza.
Quindi, utilizzare tali valori per risolvere due equazioni che consentono di determinare la lunghezza del semiasse principale Su e del semiasse secondario Sv:
e
dove
- So = deviazione standard del peso unitario
Infine, risolvere l'angolo t, generato dagli assi u e Y, mediante la seguente equazione:
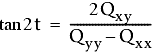
Con molta probabilità il punto di regolazione si trova all'interno dell'ellisse con un grado di confidenza del 95% o 99%.