More about triangle meshes

Why repair?

Short answer: to make a model understandable by the toolpath-generating mechanism.

Typical requirements of toolpath generators

• "No holes."

  Surfaces must be closed. While a mesh may have multiple surfaces, in each of those, all the triangles must connect with another triangle at each of its edges.

  In other words: Model must be watertight.

• "No non-manifold edges."

  Each edge of any triangle in a mesh must only ever meet with exactly one other triangle's edge. Arrangements whose cross section would look like Y-junctions or T-junctions, are not allowed.

• "Triangles must be oriented correctly."

  What counts as inside or outside is usually not derived from enclosed volume, but from the orientation of the triangles (more specifically, their normals) that enclose the volume. Normals of neighboring triangles must all, without exception, point either away from, or towards, the volume enclosed by those triangles, and must do so appropriate to the role of the shell they belong to, which could be an outside shell or an inside, hollowing shell.

• "No self-intersections."

  No triangles (or, by extension, entire shell surfaces) may intersect anywhere with themselves or each other, particularly so without a common edge along the intersection.

In other words, if you could not …

1. Take your mesh,
2. slice it in two halves anywhere and at any angle,
3. and trace each and every contour thus created with exactly one single, closed line each,
4. without ever crossing over other contour lines or itself,
5. and without the inside and outside changing sides along any stretch of line,

… then your mesh very likely needs repair.

Background

Triangle mesh files are typically lists of some form or another, containing corner point coordinates for the triangles. Adjacent triangles may use common corner points and share the same edges which results in a continuous triangle mesh.

However, many mesh file formats (like STL) do not contain any topological information about the bodies they represent. If a CAD file is imported with faults, very little information remains to consistently reconstruct missing or faulty surface automatically. Use Netfabb to detect and repair such damage and to create faultless meshes without holes, deformations, or intersections in preparation for additive manufacturing or, in fact, any other purpose that requires a certain quality in triangular mesh data.

A parametric surface and its triangulated representation

Although CAD formats have advantages, a variety of applications needs a surface representation consisting of flat triangles. These are:

• Rapid prototyping and additive manufacturing
• Accelerated rendering in multimedia applications
• Solving partial differential equations to simulate mechanical and thermal loads
• Computer Aided Design (CAD)

A good triangle mesh that can be used for 3D printing must be valid, closed, oriented and generally free from self-intersections.

Validity

Two edges of adjacent triangles which lie on top of each other are only regarded as one edge when they have equal end points. Thus, the simple mesh below consists of two triangles and has exactly five edges: four border edges and one interior edge. Border edges belong to only one triangle, while interior edges connect two triangles.

A simple mesh with 5 edges: four border edges and one interior edge.

A mesh is only regarded as valid when interior edges have the same corner points for both adjacent triangles. Only then, all neighboring triangles are connected by a whole interior edge. No neighboring triangles are split and a smooth topology is created.

This validity is an essential property of most calculations. If two edges have only one common corner point, they are defined as two border edges, even if they are on top of each other.

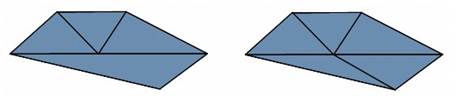
An invalid triangulation (left) compared to a valid triangulation (right).

Closedness

Parts can only be used for 3D printing when their surface is closed. This means that there are no holes and no border edges. Every edge must be attached to exactly two triangles and all neighboring triangles have to share an interior edge. Closedness may separate a mesh into several components called shells.

A closed surface (left) and a surface with holes (right)

Two disconnected (left) and two connected triangles (right)

A mesh consisting of 60 disjoint shells.

Orientability

For the conversion of triangle meshes into slice data ready for 3D printing, it is vital that the parts are oriented correctly. The orientation defines the outside and the inside of a part.

The orientation of a part is determined by the orientation of all triangles. The orientation of a triangle is in turn determined by the order in which the corner points are defined. If the orientations of all neighboring triangles conform to each other and there are no flipped triangles, a closed shell separates outside from inside. But if there are flipped triangles, this might not be possible. Thus, even closed parts can be faulty.

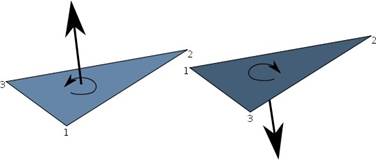
The orientation of a triangle is determined by the order of its points.

Self-Intersections

The surface of a solid body must not contain any self-intersections. These occur whenever triangles or surfaces of one part cut through each other. For many applications, self-intersections are undesired as they can cause calculations and slice and toolpath generation to produce incorrect results.

For most additive fabrication processes, three-dimensional data must be converted into 2.5-dimensional slice data. Here, self-intersections in the original data result in self-intersection in the slices. These can cause constructional failures or instabilities. Therefore, it is essential to remove self-intersections during the preparation of files.

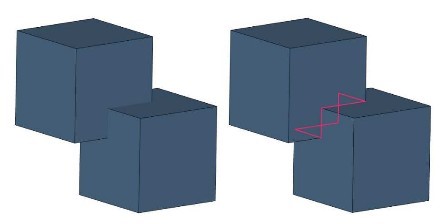
Self-Intersection: The two cubic shells cutting through each other

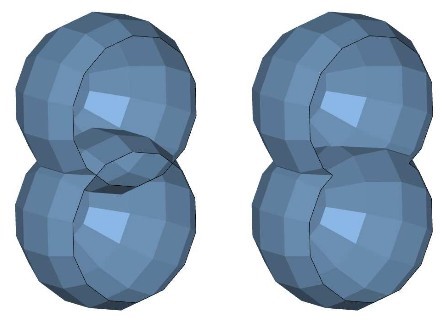
Left: A mesh consisting of two shells with self-intersection. Right: A mesh consisting of one, non-intersecting shell.