Description
The MATCF entry specifies a crushable foam material where the volumetric and deviatoric response of the material can be specified with independent plasticity models. This model may only be used with elements that use the PSOLID property type.
The pressure versus volumetric strain behavior can be defined using a piecewise linear curve where volumetric plasticity and volumetric bulking can be specified in the compression regime. The volumetric tensile behavior is elastic and defines a volumetric fracture pressure that defines a “no tension” material when the volumetric strain exceeds the Pfr value determined from the input parameters.
The deviatoric plasticity is pressure dependent and may be defined with a linear dependence on pressure or a quadratic dependence on pressure. When a linear dependence is used this model is similar to a classical Drucker-Prager material model.
Format
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| MATCF | MID | E | G | NU | RHO | A | |||
| MODEL | A0 | SLOPE | PS | YS | |||||
| EV0 | P0 | EV1 | P1 | EV2 | P2 | ||||
| ENDT |
Example
| MATCF | 35 | 5.E5 | 0.1 | 1.498E-5 | |||||
| 1 | 100 | 10 | |||||||
| 0.0 | 0.0 | 0.001 | 200 | 0.003 | 200 | 0.005 | 400 | ||
| 0.007 | 800 | 0.009 | 1800 | 0.010 | 3800 | ENDT |
| Field | Definition | Type | Default |
|---|---|---|---|
| MID | Material identification number | Integer > 0 | Required; See Remarks 1 and 2 |
| E | Young's modulus | Real ≥ 0.0 or blank | See Remarks 3 and 4 |
| G | Shear modulus | Real ≥ 0.0 or blank | See Remarks 3 and 4 |
| NU | Poisson's ratio | -1.0 < Real ≤ 0.5 or blank | See Remark 4 |
| RHO | Mass density | Real ≥ 0.0 | Required |
| A | Thermal expansion coefficient | Real or blank | 0.0 |
| MODEL | Yield Stress Dependence on Pressure:
1 = Linear 2 = Quadratic 3 = Elastic/Plastic Strain Softening Compression |
Integer > 0 | 1, See Remark 5 |
| A0 | Yield stress at zero pressure | Real ≥ 0.0 | Required; See Remarks 5 and 6 |
| SLOPE | Slope of Yield Stress vs. Pressure curve | Real ≥ 0.0 or blank | 0.0; See Remarks 5 and 6 |
| PS | Pressure at which SLOPE is specified (ignored if MODEL=1) | Real ≥ 0.0 or blank | 0.0; See Remark 6 |
| EVn | Volumetric strain | Real ≥ 0 | See Remark 7 |
| Pn | Pressure value | Real ≥ 0 | See Remark 7 |
Remarks
- The material identification number must be unique for all MATi entries.
- This material may only be used with Solid element types.
- Either E or G must be specified (not blank).
- If any one of E, G, or NU is blank, it will be computed to satisfy the identity E = 2(1 + NU)G; otherwise, values supplied by the user will be used.
- The deviatoric yield stress is pressure dependent and the dependency can be either linear or quadratic. For the linear case (MODEL=1), shown in Figure 1, the user specifies the yield at zero pressure, A0, and a constant slope for the yield stress as a function of pressure, SLOPE. This defines a conical shape of the yield stress versus pressure surface as shown in Figure1. For the quadratic case (MODEL=2), shown in Figure 2, the user specifies A0, SLOPE, the pressure as the specified slope, PS, and the yield at the specified slope, YS. The coefficients A1 and A2 of the quadratic dependency are automatically determined from the user supplied parameters. The value of the tensile volumetric fracture pressure is determined such that the quadratic curve passes through the user supplied value of A0 and matches the SLOPE provided at the pressure (PS,YS).
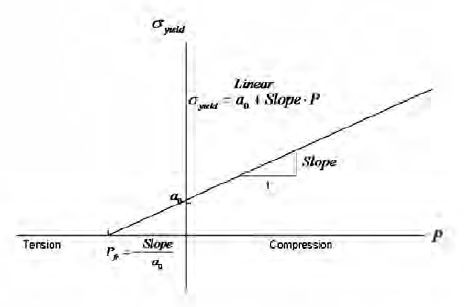
Figure 1: Linear Dependence of Yield Stress on Pressure (MODEL=1)
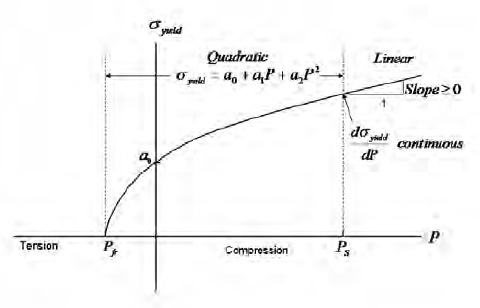
Figure 2: Quadratic Dependence of Yield Stress on Pressure (MODEL=2)
- A value of zero is allowable for the SLOPE for the linear case (CMODEL=1). This specifies a constant yield stress, independent of pressure as shown in Figure 3. In this case, the tensile volumetric fracture pressure is assumed to be infinite (i.e. no tensile failure occurs).
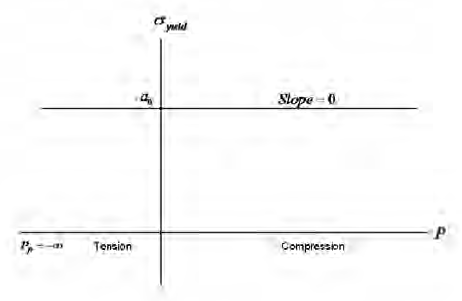
Figure 3: No Pressure Dependence of Yield Stress (MODEL = 1)
- The value of the pressure at which the slope is defined (PS) may be zero. In this case, only the tensile range of pressures uses the quadratic form for the yield stress dependence as shown in Figure 4.
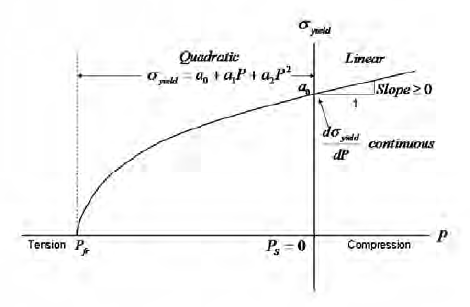
Figure 4: Quadratic Case With PS Value of Zero (MODEL = 2)
- The EVn, Pn points define the piecewise linear behavior of the pressure versus volumetric strain in compression as shown in Figure 5. At least 2 points must be provided, in which case a linear response in compression is defined. The first point (EV0, PV0) must be defined at zero strain and pressure. The tensile volumetric response is purely elastic up to the point of tensile volumetric fracture defined by
Pfr, which is determined from the deviatoric coefficients as described in Remark 1.
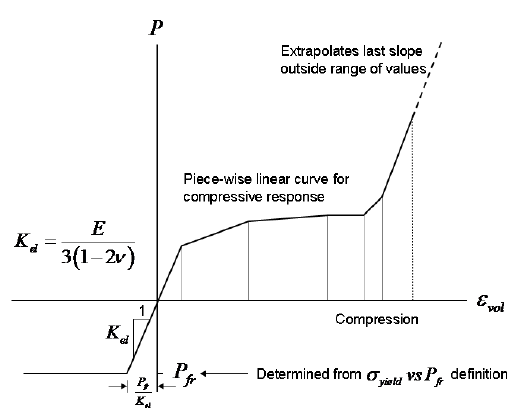
Figure 5: Pressure vs. Volumetric Response Curve
