Description
The MATR1 allows you to define a rigid body through the use of material identification number.
The MATR1 entry allows you to declare that a material is rigid. For a rigid material, all properties for that material except the density are ignored.
A part (set of elements) that references the material identification number on a MATR1 entry will constitute a rigid body. All of the nodes associated with the elements in the part will be used to define the rigid body. Autodesk Explicit automatically determines properties (i.e. location of the center of mass, total mass, and rotary inertia tensor about the center of mass) of the rigid body. An internal reference node for the rigid body is created with six degrees of freedom (three translations and three rotations).
Boundary conditions can be defined for the rigid body using the SPCR and SPCRD entries. Any boundary condition applied to nodes of the elements will be ignored. You must specify the boundary conditions for the rigid body using the reference node through the SPCR and SPCRD entries.
Format
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| MATR1 | MID | CID | M | ||||||
| I11 | I21 | I22 | I31 | I32 | I33 |
Example
| MATR1 | 25 | 4 | 5.35 |
| Field | Definition | Type | Default |
|---|---|---|---|
| MID | Material identification number of a MAT1 or MAT8 entry. | Integer > 0 | Required |
| CID | Coordinate system identification number. | Integer ≥ 0 | 0 |
| M | Mass value to be added to computed mass for rigid body. | Real or blank | 0.0 |
| Iij | Mass moments of inertia added to the calculated inertia tensor for the rigid body. The inertia terms are defined in terms of the coordinate system referenced by the coordinate system identification number CID. See Remark 3. | I11, I22, and I33, Real ≥ 0.0; I21, I31, and I32, Real ≥ 0.0. | 0.0 |
Remarks
- The continuation may be omitted.
- The coordinate system identification number, CID, is used for the definition of the inertia terms.
- The form of the inertia matrix about its center of mass is taken as:
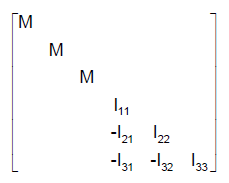
In the above equations:
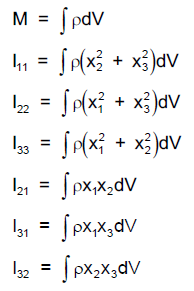
The mass M is added to the mass that is initially computed for the rigid body, Mc. The total mass for the rigid body, M, is M+Mc.
The x1, x2, x3 are components of distance from the center of gravity in the coordinate system defined in field 4. Only the magnitude of Iij should be supplied; the negative signs for the off-diagonal terms are supplied automatically. The inertia terms are transformed to the principal coordinate system for the inertia tensor for the rigid body.
